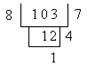第一章 代数、三角公式与初等函数

 

这里收集和整理了初等代数(代数方程部分见第三章)，平面三角与球面三角的一些常用公式，同时也介绍了一些常见的初等函数(一个实自变量)的简单性质与图形，所以本章基本上包括了中等学校里的代数学和三角学的主要内容.

 

§1 代 数 公 式

 

一、 数的扩张、分类及其基本运算规则

 

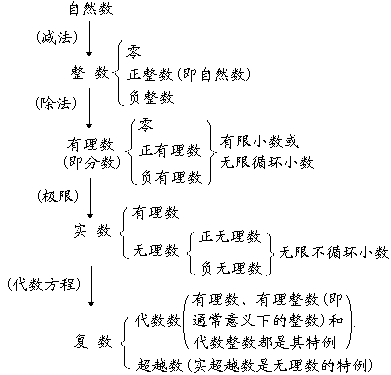
1. 数的扩张与分类表

2. 实数四则运算规则

[加减法规则] 同号两数相加，绝对值相加，符号与加数同；异号两数相加，绝对值相减(大的减小的)，符号与绝对值大的加数同；任何实数和零相加，等于实数本身.减法是加法的逆运算，两个数相减只要把减数变成同它符号相反的数，即可按加法规则运算.

[乘除法规则] 同号两数相乘，绝对值相乘，符号为正；异号两数相乘，绝对值相乘，符号为负；任何数与零相乘等于零；任何数与1相乘等于它自己.除法是乘法的逆运算，同号两数相除，绝对值相除，符号为正；异号两数相除，绝对值相除，符号为负；任何数除以1等于它自己；零除以任何不等于零的数等于零；零不能做除数.

[四则混合运算规则] 先乘除，后加减；先括号内，后括号外.

3. 数的三个基本运算律

[交换律]    

       [结合律]  

       [分配律]

4. 乘方与开方

[乘方]  n个数a相乘

                                             n个

称为a的n次(乘)方，又称为a的n次幂.a称为幂底数，n称为幂指数.

从乘法的符号规则直接得出乘方的符号规则：正数的任何次方为正数；负数的偶次方为正数；负数的奇次方为负数；零的任何次方为零.

规定不等于零的数的零次方等于1，即a⁰=1，a¹0.

[开平方]  若a²=b，则a称为b的平方根，记为，求平方根的运算称为开平方.开平方的一般方法用下面例子说明.

例  求316.4841的平方根.

解  第一步,先将被开方的数，从小数点位置向左右每隔两位用逗号“，”分段，如把数316.4841分段成3,16.48,41.第二步，找出第一段数字的初商，使初商的平方不超过第一段数字，而初商加1的平方则大于第一段数字，本例中第一段数字为3，初商为1，因为1²=1<3，而(1+1)²=4>3.第三步，用第一段数字减去初商的平方，并移下第二段数字，组成第一余数，在本例中第一余数为216.第四步，找出试商，使(20´初商+试商)´试商不超过第一余数，而[20´初商+(试商+1)]´(试商+1)则大于第一余数.第五步，把第一余数减去(20´初商+试商)´试商，并移下第三段数字，组成第二余数，本例中试商为7，第二余数为2748.依此法继续做下去，直到移完所有的段数，若最后余数为零，则开方运算告结束.若余数永远不为零，则只能取某一精度的近似值.第六步，定小数点位置，平方根小数点位置应与被开方数的小数点位置对齐.本例的算式如下：

[开立方]  若a³=b，则a称为b的立方根，记为，求立方根的运算称为开立方.

一个数的平方根和立方根可从“平方根表”和“立方根表”中查到.

5. 实数进位制

[进位制的基与数字]  任一正数可表为通常意义下的有限小数或无限小数，各数字的值与数字所在的位置有关，任何位置的数字当小数点向右移一位时其值扩大10倍，当小数点向左移一位时其值缩小10倍.例如

一般地，任一正数a可表为

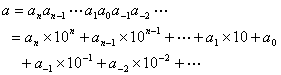
这就是10进数，记作a₍₁₀₎，数10称为进位制的基，式中a_i在{0,1,2,L,9}中取值，称为10进数的数字，显然没有理由说进位制的基不可以取其他的数.现在取q为任意大于1的正整数当作进位制的基，于是就得到q进数表示

  (1)

式中数字a_i在{0,1,2,L,q-1}中取值，a_na_n-1La₁a₀称为q进数a_(q)的整数部分，记作[a_(q)];

a_-1a_-2L称为a_(q)的分数部分，记作{a_(q)}.常用进位制，除10进制外，还有2进制、8进制、16进制等，其数字如下

                               2进制         0, 1

                               8进制         0, 1, 2, 3, 4, 5, 6, 7

                             16进制         0, 1, 2, 3, 4, 5, 6, 7, 8, 9

                                                 

[2，8，16进制的加法与乘法表]

8进制加法表

+	0	1	2	3	4	5	6	7
0	00	01	02	03	04	05	06	07
1	01	02	03	04	05	06	07	10
2	02	03	04	05	06	07	10	11
3	03	04	05	06	07	10	11	12
4	04	05	06	07	10	11	12	13
5	05	06	07	10	11	12	13	14
6	06	07	10	11	12	13	14	15
7	07	10	11	12	13	14	15	16

8进制乘法表

	0	1	2	3	4	5	6	7
0	00	00	00	00	00	00	00	00
1	00	01	02	03	04	05	06	07
2	00	02	04	06	10	12	14	16
3	00	03	06	11	14	17	22	25
4	00	04	10	14	20	24	30	34
5	00	05	12	17	24	31	36	43
6	00	06	14	22	30	36	44	52
7	00	07	16	25	34	43	52	61

16进制加法表

+	0	1	2	3	4	5	6	7	8	9
0	00	01	02	03	04	05	06	07	08	09
1	01	02	03	04	05	06	07	08	09		0					10
2	02	03	04	05	06	07	08	09							10	11
3	03	04	05	06	07	08	09							10	11	12
4	04	05	06	07	08	09							10	11	12	13

16进制加法表

5	05	06	07	08	09							10	11	12	13	14
6	06	07	08	09							10	11	12	13	14	15
7	07	08	09							10	11	12	13	14	15	16
8	08	09							10	11	12	13	14	15	16	17
9	09							10	11	12	13	14	15	16	17	18
							10	11	12	13	14	15	16	17	18	19
						10	11	12	13	14	15	16	17	18	19
					10	11	12	13	14	15	16	17	18	19
				10	11	12	13	14	15	16	17	18	19
			10	11	12	13	14	15	16	17	18	19
		10	11	12	13	14	15	16	17	18	19

16进制乘法表

+	0	1	2	3	4	5	6	7	8	9
0	00	00	00	00	00	00	00	00	00	00	00	00	00	00	00	00
1	00	01	02	03	04	05	06	07	08	09
2	00	02	04	06	08				10	12	14	16	18
3	00	03	06	09			12	15	18			21	24	27
4	00	04	08		10	14	18		20	24	28		30	34	38
5	00	05			14	19		23	28		32	37		41	46
6	00	06		12	18		24		30	36		42	48		54
7	00	07		15		23		31	38		46		54		62	69
8	00	08	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	00	09	12		24		36		48	51		63		75		87
	00		14		28	32		46	50		64		78	82		96
	00		16	21		37	42		58	63		79	84
	00		18	24	30		48	54	60		78	84	90
	00			27	34	41			68	75	82
	00				38	46	54	62	70
	00							69	78	87	96

 

[8-2，16-2数字转换表]

 

8进数	0	1	2	3	4	5	6	7
2进数	000	001	010	011	100	101	110	111
16进数	0	1	2	3	4	5	6	7
2进数	0000	0001	0010	0011	0100	0101	0110	0111
16进数	8	9
2进数	1000	1001	1010	1011	1100	1101	1110	1111

 

[各种进位制的相互转换]

1^°  qÕ10转换  适用通常的10进数四则运算规则，根据公式(1)，可以把q进数a_(q)转换为10进数表示.例如

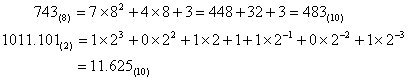
2^°  10Õq转换  转换时必须分为整数部分和分数部分进行.

对于整数部分其步骤是：

(1) 用q去除[a₍₁₀₎]，得到商和余数.

(2) 记下余数作为q进数的最后一个数字.

(3) 用商替换[a₍₁₀₎]的位置重复(1)和(2)两步，直到商等于零为止.

       对于分数部分其步骤是：

(1)用q去乘{a₍₁₀₎}.

(2)记下乘积的整数部分作为q进数的分数部分第一个数字.

(3)用乘积的分数部分替换{a₍₁₀₎}的位置，重复(1)和(2)两步，直到乘积变为整数为止，或直到所需要的位数为止.例如：

103.118₍₁₀₎=147.074324L₍₈₎

                                   

3^°  pÕq转换  通常情况下其步骤是：a_(p)Õa₍₁₀₎Õa_(q).如果p,q是同一数s的不同次幂，其步骤是：a_(p)Õa_(s)Õa_(q).例如，8进数127.653₍₈₎转换为16进数时，由于8=2³，16=2⁴，所以s=2，其步骤是：首先把8进数的每个数字根据8-2转换表转换为2进数(三位一组)

127.653₍₈₎=001 010 111.110 101 011₍₂₎

然后把2进数的所有数字从小数点起(左和右)每四位一组分组，从16-2转换表中逐个记下对应的16进数的数字，即

 

二、复数

 

1. 复数的概念

[实部与虚部·模与辐角·共轭复数]  复数z一般表示为z=a+ib，其中称为虚数单位，a和b均为实数，分别称为z的实部和虚部，记为a=Re z，b=Im z.

两个复数只有当实部和虚部分别相等时才相等.

称为复数z的模.

称为复数z的辐角，所以，一个复数有无穷多个辐角，但其中一个叫做主辐角，记为arg z，它满足

                              0≤arg z<2p

并有            Arg z=arg z+2kp               (k=0,±1,±2,L)

与互为共轭复数.

[虚数单位的乘方]

    2．复数的表示法

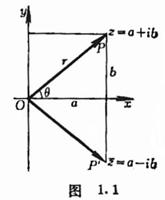
[坐标表示法]  复数z=a+ib可与直角坐标(a,b)建立一一对应(图1.1).

[矢量表示法]  把a，b视为矢量在x轴和y轴上的投影，则矢量(图1.1)可表示复数z=a+ib，与P点关于x轴对称的点记为，矢量表示共轭复数.

[三角表示法]  

                          

[指数表示法]  

   3．复数的运算

[代数式运算]

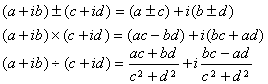
[三角式运算]  设

                              

则                                  

                                          

                                                 

当r₁=1时，得，这个公式叫做德·莫弗公式.

[指数式运算]  设

                                                

则                                   

 

三、数列与简单级数

 

1．数列与级数的概念

依照某种规则排列着的一列数

                         a₁, a₂, a₃, L, a_n, L

称为数列，记作{a_n}.若把这一列数用和号联接起来：

                         a₁+a₂+a₃+L+a_n+L

它称为级数，记作.a_n称为该数列或相应级数的通项（或称为一般项）.

2．等差数列与等差（算术）级数

a₁, a₁+d, a₁+2d, a₁+3d, L   (d为常数)

称为公差为d的等差数列.与等差数列相应的级数称为等差级数，又称算术级数.

通项公式     

前n项和             

等差中项             

3．等比数列与等比（几何）级数

a₁, a₁q, a₁q², a₁q³, L     (q为常数)

称为公比为q的等比数列.与等比数列相应的级数称为等比级数，又称几何级数.

通项公式             

前n项和             

等比中项             

无穷递减等比级数的和                      

4．算术-几何级数

            ≥1)

              

5．调和级数

1^o  若为等差级数，则a+b+c+L称为调和级数.调和中项为

                             

2^o  设A, G, H分别为某两个数的等差中项、等比中项和调和中项，则

AH=G²

6．高阶等差级数

设有一数列

                           a₁, a₂, L, a_n, L                                  (1)

如果接连地从它的后一项减去前一项，那末就得到原数列(1)的第一次差构成的数列

a₂-a₁, a₃-a₂, L, a_n-a_n-1, L                            (2)

再接连地将(2)的后一项减去前一项，又得到数列(1)的第二次差构成的数列.依次类推：

                       a₁                                    a₂                                    a₃                        a₄                  L

   第一次差               d₁=Da₁                      Da₂                        Da₃                   L

   第二次差                             d₂=D²a₁                    D²a₂                      L

   第三次差                                            d₃=D³a₁                      L

                                                                                LL

式中                                             

如果做了r次，数列(1)的每个第r次差都相等，那末以后各次差都等于零，则称数列(1)为r阶等差数列.与这样的数列相应的级数称为r阶等差级数.一阶等差级数也就是通常的算术级数.

设(1)是r阶等差数列，并设d₁为(1)的第一次差构成的数列的首项，d₂为(1)的第二次差构成的数列的首项，L，d_r为(1)的第r次差构成的数列的首项，则有

通项公式  (n>r)

前n项和

7．某些级数的部分和

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

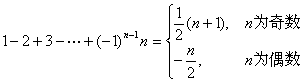
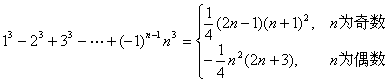
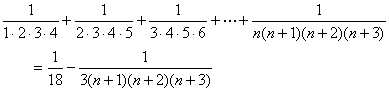
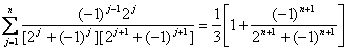
四、乘法与因式分解公式

 

 

 

 

 

 

 

 

 

 

 

五、分式

 

   1. 分式运算

                                                   

                                                       

                                                       

2. 部分分式

任一既约真分式(分子与分母没有公因子，分子次数低于分母次数)都可唯一地分解成形如或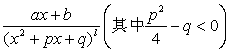的基本真分式之和，其运算称为部分分式展开.若为假分式(分子次数不低于分母次数)，应先化为整式与真分式之和，然后再对真分式进行部分分式展开.部分分式的各个系数可以通过待定系数法来确定.下面分几种不同情况介绍.

设                           

                               

[线性因子重复]

1^o 

式中N(x)的最高次数r≤m-1；A₀，A₁，L，A_m-1为待定常数，可由下式确定：

             

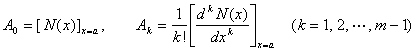
2^o 

式中A₀，A₁，L，A_m为待定常数，可由下式确定：

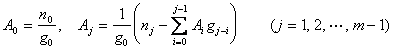
≤s-1

其系数f_j与m有关，由下表确定：

m	fj   (j=0, 1, 2, L, k; k≤s-1)
1
2
3
M	LLLLLLLL
m

   例 

解  依上述公式算出

          

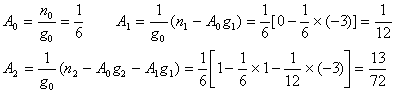
此时m=3，

   

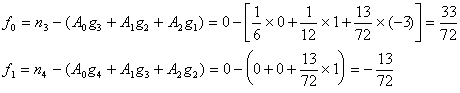
所以得到

3^o 

作变换y=x-a，则N(x)=N₁(y), G(x)=G₁(y), 上式变为

                  

用上述1^o，2^o的方法确定出A₀, A₁, L, A_m-1和F₁(y)，再将y=x-a代回.也可按下式来确定系数A₀, A₁, L, A_m-1：

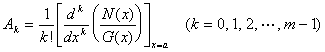
[线性因子不重复]

1^o  

式中N(x)的最高次数r≤2，a¹b¹c；A, B, C为待定常数，可由下式确定：

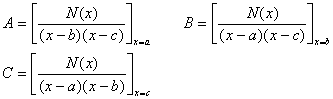
2^o 

式中多项式F(x)的最高次数k≤s-1；A, B为待定常数，用下式确定：

                   

A, B确定后，再用等式两边多项式同次项系数必须相等的法则来确定F(x)的各项系数.

例 

解  依上述公式算得

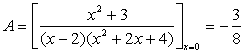
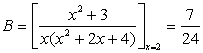
把A,B代入原式，通分并整理后得

比较等式两边同次项系数得

所以有

[高次因子]

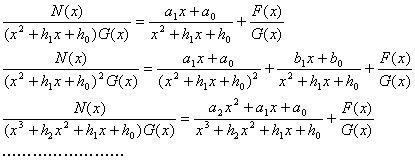
[计算系数的一般方法]

                  

1^o  等式两边乘以D(x)化为整式，各项按x的同次幂合并，然后列出未知系数的方程组，解出而得.

2^o  等式两边乘以D(x)化为整式，再把x用简单的数值(如x=0, 1, -1等)代入，然后列出未知系数的方程组，解出而得.

六、比例

 

1^o  若(或写为a:b=c:d)，a, b, c, d都不等于零，则

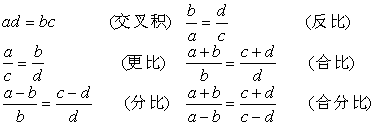
2^o  若，则

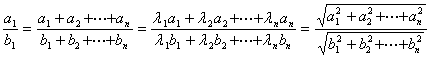
式中l_i(i=1, 2, L, n)为一组任意的常数，b_i(i=1, 2, L, n)都不等于零.

3^o  若y与x成正比，(记作yµx)，则

若y与x成反比，，则

若y与x成正比，y与z也成正比(即yµx, yµz)，则x与z成正比，即

且y与xz成正比，即

 

七、根式

 

1. 根式的概念

[方根与根式]  数a的n次方根是指求一个数，它的n次方恰好等于a.a的n次方根记为(n为大于1的自然数).作为代数式，称为根式.n称为根指数，a称为根底数.在实数范围内，负数不能开偶次方，一个正数开偶次方有两个方根，其绝对值相同，符号相反.

[算术根]  正数的正方根称为算术根.零的算术根规定为零.

[基本性质]  由方根的定义，有

   2. 根式运算

[乘积的方根]  乘积的方根等于各因子同次方根的乘积；反过来，同次方根的乘积等于乘积的同次方根，即

≥0,b≥0)

[分式的方根]  分式的方根等于分子、分母同次方根相除，即

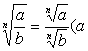≥0,b>0)

[根式的乘方]                     ≥0)

[根式化简]

≥0)

                                                                    ≥0,d≥0)

                                                                    ≥0,d≥0)

[同类根式及其加减运算]  根指数和根底数都相同的根式称为同类根式，只有同类根式才可用加减运算加以合并.

 

八、不等式

 

   1. 简单不等式

1^o  若a>b，则

      

2^o  若，且b、d同号，则

2. 有关绝对值的不等式

1^o  若a, b, L, k为任意复数，则

≤

                          ≤

2^o  若a, b为任意复数，则

≤≤

3^o  若≤，则

≤≤特别有≤≤

4^o  若≥，则

或

3. 有关三角函数、指数函数、对数函数的不等式

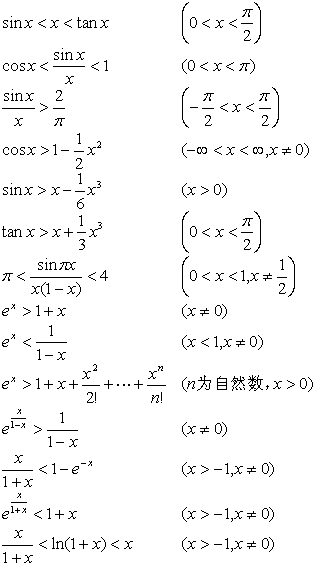
特别取，有

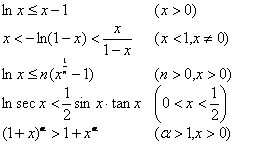
 (以下各式变数z为复数)

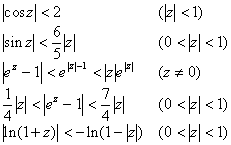
4. 某些重要不等式

[算术平均值与几何平均值不等式]

1^o  几个数的算术平均值的绝对值不超过这些数的均方根，即

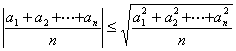
等号只当时成立.

2^o  设a₁, a₂, L, a_n均为正数，则它们的几何平均值不超过算术平均值，即

等号只当时成立.

3^o  对n个正数a₁, a₂, L, a_n的加权平均值，有

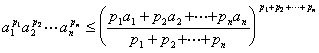
等号只当a₁=a₂=L=a_n时成立.

4^o  设a₁, a₂, L, a_n为正数，又，则有

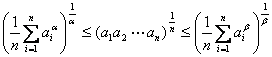
[柯西不等式]  设a_i, b_i(i=1, 2, L, n)为任意实数，则

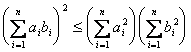
等号只当时成立.这个不等式表明一个角(取实数值)的余弦值总是小于1的，或者说二矢量内积小于二矢量长度之积.

[赫尔德不等式]

1^o  设a_i, b_i, L, l_i(i=1, 2, L, n)为正数，又a, b, L, l为正数，且a+b+L+l=1，则

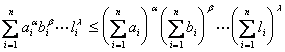
等号只当时成立.

2^o  设a_i, b_i (i=1, 2, L, n)为正数，又k>0, k¹1, 与k共轭，即，或，则

等号只当时成立.

[闵可夫斯基不等式]  设a_i, b_i>0 (i=1, 2, L, n)，又r>0, r¹1, 则

等号只当时成立.当r=2时，此不等式也称为三角形不等式，它表明三角形两边之和大于第三边.

[契贝谢夫不等式]  设a_i>0, b_i>0 (i=1, 2, L, n).若a₁£a₂£L£a_n, 且b₁£b₂£L£b_n, 或a₁³a₂³L³a_n, 且b₁³b₂³L³b_n, 则

若a₁£a₂£L£a_n而b₁³b₂³L³b_n，则

[詹生不等式]  设a_i>0 (i=1, 2, L, n)，且0<r£s，则

[伯努利不等式]  设a>1，自然数n>1，则

特别令，则

   5. 二次不等式解法

的解 (设)

	D>0	D=0	D<0
a>0
a<0		无解	无解

 

九、阶乘、排列与组合

 

   1. 阶乘

[阶乘的定义]  设n为自然数，则

称为n的阶乘.并且规定0!=1.又定义

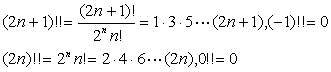
[斯特林公式]

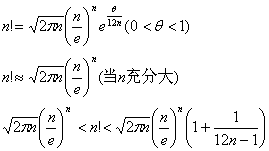
[阶乘有限和公式]

   2. 排列

[选排列]  从n个不同的元素中，每次取出k个(k£n)不同的元素，按一定的顺序排成一列，称为选排列.其排列种数为

[全排列]  从n个不同的元素中，每次取出n个不同的元素，按一定的顺序排成一列，称为全排列.其排列种数为

[有重复的排列]  从n个不同的元素中，每次取出k个元素(k£n)，允许重复，这种排列称为有重复的排列.其排列种数为

[不尽相异元素的全排列]  如果在n个元素中，有n₁个元素彼此相同，又有n₂个元素彼此相同，L，又有n_m个元素彼此相同(n₁+n₂+L+n_m=n)，那末这n个元素的全排列称为不尽相异元素的全排列.其排列种数为

[环状排列]  从n个不同元素中，每次取出k个元素，仅按元素之间的相对位置而不分首尾地围成一圈，这种排列法称为环状排列.其排列种数为

   3. 组合

[通常意义下的组合]  从n个不同的元素中，每次取出k个不同的元素，不管其顺序合并成一组，称为组合.其组合种数为

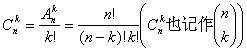
并且规定.

[多组组合]  把n个不同的元素分成m组，第i组有n_i个不同的元素，即，这样分组的种数为

通常意义下的组合是其特例.

[有重复的组合]  从n个不同元素中，每次取出k个元素，允许重复，不管其顺序合并成一组，这种组合称为有重复的组合，其组合种数为

[组合公式]

 

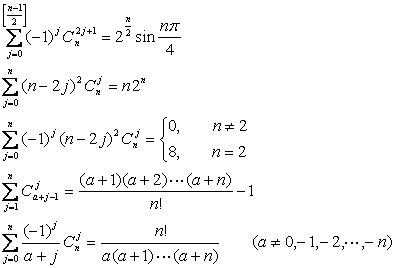
十、杨辉三角形与多项式定理

 

[二项式定理]

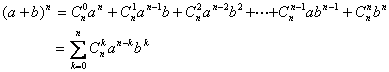
式中n为正整数，称为二项系数.

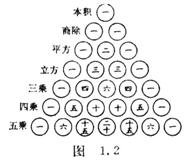
[杨辉三角形]  我国南宋时期数学家杨辉在他所著的《详解九章算法》(1261年)中记载着有关二项系数的研究.在二项式定理中，当n分别取0, 1, 2, 3, 4, 5, 6时，其二项系数表示成图1.2，即所谓“杨辉三角形”.法国人帕斯卡也有类似结果(1650年)，故外国书刊中称之为“帕斯卡三角形”，但比杨辉晚了近四百年.

[多项式定理]

和式中每一数组(p, q, L, s)对应一项，这个数组满足0£p£n, 0£q£n, L, 0£s£n, p+q+L+s=n, S是对于所有这样的数组求和.

 

十一、数学归纳法与抽屉原理

 

[数学归纳法]  对于包含整数n的公式，即从某一整数起对后面所有整数n都成立的公式，有时可用数学归纳法来证明.其步骤如下：

1^o  验证n取第一个值n₀时(如n₀=0, 1或2等)公式成立.

2^o  假定当n=k时公式成立，验证当n=k+1时公式也成立.

因为公式当n=n₀时成立，所以由2^o可知，当n=n₀+1时公式也成立；再由2^o可知，当n=n₀+1+1=n₀+2时公式也成立，如此继续推下去可知，对一切大于n₀的整数n公式都成立.

[抽屉原理]  n+1个物体放入n个抽屉里，至少有一个抽屉有两个以上的物体，这个原理称为抽屉原理，它在证明某些存在性定理时很有用.抽屉原理分以下三种形式：

1^o  n+1个元素分成n组，必有一组至少包含两个元素.

2^o  m个元素分成n组(m>n为正整数)，必有一组至少包含个元素([x]表示x的整数部分).

3^o  无限多个元素分成有限组，必有一组包含无限多个元素.