§3 代数方程的特殊解法
阿贝耳证明了五次及更高次的一般方程没有代数解法.可是阿贝耳定理并没有回答这个问题:每个给定的具体方程有没有代数解法.伽罗瓦证明了:存在用代数方法不能解的具体整系数代数方程.例如
x5-x+1=0
伽罗瓦还找出方程能用根式求解的充分必要条件.
1.求有理根
根据上一节中“整根与有理根”的性质,可以求某些具体方程的有理根.
例 求方程![]() 的有理根.
的有理根.
解 因为该方程的有理根![]() 的p和q都是2的约数,所以它们是1,-1,2和-2.因此
的p和q都是2的约数,所以它们是1,-1,2和-2.因此![]() 的可能值为1,-1,
的可能值为1,-1,![]() 2和-2.用综合除法(见§2,一)
2和-2.用综合除法(见§2,一)
检验:
1) 2 -3 2 2 -1) 2 -3 2 2
2 -1 1 -2 5 -7
![]()
![]() 2 -1 1
3
2 -5 7 -5
2 -1 1
3
2 -5 7 -5
![]() 2
-3
2
2
2
-3
2
2 ![]() 2 -3
2 2
2 -3
2 2
![]()
![]() 1 -1
1 -1 ![]() -1
2 -2
-1
2 -2
2 -2
1 ![]() 2
-4
4 0
2
-4
4 0
所以![]() 为已知方程的一个有理根.
为已知方程的一个有理根.
原式除以![]() ,得商式
,得商式
![]() 即
即 ![]()
塔顶判别式4-8<0,它的两个根是一对共轭复根.因此原方程只有一个有理根![]() .
.
2.解三项方程
形如
au2n+bun+c=0
的方程称为三项方程,其中a,b,c,n都不等于零,n为整数.它可用根式解.令un=x,得二次方程ax2+bx+c=0.
例 解方程
![]()
解 令![]() ,则得
,则得![]() ,它的根是
,它的根是![]() 和
和![]() .从
.从![]() 得
得![]() .所以
.所以![]() .代入原方程检验,可知这四个数是方程的根.
.代入原方程检验,可知这四个数是方程的根.
3.解倒数方程
形如
axn+bxn-1+cxn-2+L+cx2+bx+a=0
(其中xn-k和xk项的系数相同)的方程称为倒数方程.倒数方程的任一根不等于零.
1° 偶数次(n=2k)倒数方程两边除以xk,再令z=x+![]() ,则原方程可化为z的k次方程,解此方程,得z的值,然后对应的x值可由二次方程
,则原方程可化为z的k次方程,解此方程,得z的值,然后对应的x值可由二次方程
x2-zx+1=0
求出.
2° 解奇数次(n=2k+1)倒数方程归结为解偶数次倒数方程.
例 解方程
![]()
解 ![]() 为原方程的一个根,把方程除以
为原方程的一个根,把方程除以![]() ,得4次倒数方程:
,得4次倒数方程:
![]()
把它除以![]() ,然后并项,得
,然后并项,得
![]()
令![]() ,则
,则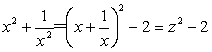 ,从而上式变为
,从而上式变为
![]()
由此得![]() .因而有确定
.因而有确定![]() 的两个方程:
的两个方程:
![]() 和
和 ![]()
由此得
![]()
4.解二项方程
形如 xn-A=0
的方程称为二项方程.它的n个根就是复数A的n次方根.
 如果把A写为
如果把A写为
A=r(cosθ+isinθ)
则方程xn-A=0的n个根是
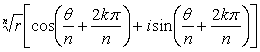 (k=0,1,2,L,n-1)
(k=0,1,2,L,n-1)
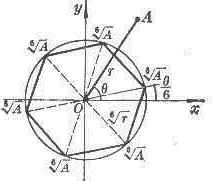
几何说明:复平面上与数r(cosθ+isinθ)的n次方根对应的点是一个正n边形的顶点,这些顶点在以原点为中心,以![]() 为半径的圆上.而这个n边形的顶点之一有辐角
为半径的圆上.而这个n边形的顶点之一有辐角![]() .图3.1表示n=6的情形.
.图3.1表示n=6的情形.
若A=1,则xn=1的解ξ称为n次单位根.n个n次单位根为
cos![]() +isin
+isin![]() (k=0,1,2,L,n-1) 图 3.1
(k=0,1,2,L,n-1) 图 3.1
如果ξ是其中一个n次单位根,那末n个n次单位根是1, ξ,ξ2,L,ξn-1,它们在几何上表示为单位圆的一个内接正n边形的顶点.