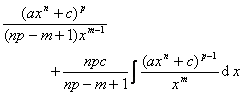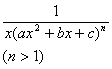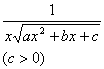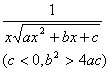第六章 积 分 学
这一章综述了单变量函数的常义积分、广义积分、含参数积分的基本概念、性质和计算方法,收集了求不定积分、定积分、多重积分、曲线积分、曲面积分的有关公式,主要的积分不等式以及积分的某些近似计算公式,简要地列举了积分在实际中的各种应用;编制了不定积分表和定积分表.
§1单变量函数的积分
一、积分基本概念
[不定积分(原函数)] 如果在给定的区间[a ,b]上
![]()
那末F (x)称为f(x)在区间[a,b]上的一个原函数.
如果f (x)有一个原函数F (x),那末它一定有无穷多个原函数,它们是形如
![]()
(式中C是任意常数)的函数族,所以用记号
![]()
表示f (x)的原函数全体,称为f (x)的不定积分.
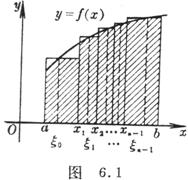
[定积分·黎曼积分] 设在区间[a,b]上给定了函数f (x).用任意方法把区间[a,b]分成若干部分,其分点为![]() ,并设λ是
,并设λ是![]() (i=0,1,2,…,n-1)中最大的.在每一个小区间[
(i=0,1,2,…,n-1)中最大的.在每一个小区间[![]() ]上任取一点
]上任取一点![]() (i=0,1,2,…,n-1),作和
(i=0,1,2,…,n-1),作和![]() (图6.1).当λ→0时,如果极限
(图6.1).当λ→0时,如果极限
![]()
存在,那末这个极限称为函数f(x)在区间[a,b]上的定积分,记作
![]()
此时,函数f(x)称为区间[a,b]上的可积函数(黎曼可积),a和b分别称为积分的下限和上限,f(x)称为被积函数,x是积分变量,“![]() ”是积分号.
”是积分号.
|
|
[牛顿-莱布尼茨公式] 若函数f(x)在区间[a,b]上连续,或分段连续,则f(x)在[a,b]上有原函数,设F(x)是f(x)在[a,b]上的一个原函数,则
![]()
这称为牛顿-莱布尼茨公式,或微积分学基本定理,它指出了定积分与不定积分的内在联系.
[可积函数及其性质]
1° 若函数f(x)在区间[a,b]上连续,则f(x)是可积的.
2° 若函数f(x)在[a,b]上有界,且只有有限多个间断点,则f(x)是可积的.
3° 单调有界函数一定是可积的.
4° 可积函数一定是有界的.
5° 若函数f(x)可积,则|f(x)|与kf(x)(k为常数)也可积.
6° 若函数f(x),g(x)可积,则其和、差、乘积也可积.
7° 若函数f(x)在[a,b]上可积,则f(x)在[a,b]中的任一部分区间[α,β]上也可积.反之,若把[a,b]分割成若干部分区间,并分别在每个部分区间上f(x)可积,则它在整个区间[a,b]上可积.
[积分中值定理]儍儍儍儍
|
|
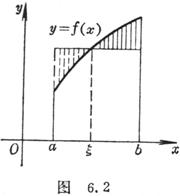
1° 若函数f(x)在区间[a,b]上连续(图6.2),则在区间[a,b]内至少存在一个数ξ(a<ξ<b),使得
![]()
2° 若函数f(x),g(x)在区间[a,b]上有界且可积,f(x)连续,g(x)在区间[a,b]内不变号,则在区间[a,b]内至少存在一个数ξ(a<ξ<b),使得
![]()
这称为关于积分的第一中值定理.
3° 若函数f(x),g(x)在区间[a,b]上有界且可积,而f(x)在[a,b]上是单调的,则在区间[a,b]内至少存在一个数ξ(a<ξ<b),使得
![]()
这称为关于积分的第二中值定理.
4° 除此条件而外,若f(x)非负单调下降(广义的),则
![]() (a<ξ<b)
(a<ξ<b)
若f(x)非负单调上升(广义的),则
![]() (a<ξ<b)
(a<ξ<b)
二、积分不等式
设f(x),g(x)在区间[a,b]上可积,则有下列不等式:
1° 若在区间[a,b]上,f(x)≤g(x),则
![]() ≤
≤![]()
2° 设![]() ,则
,则
m≤![]() ≤M
≤M
3° ![]() ≤
≤![]()
4° 施瓦兹不等式
![]() ≤
≤![]()
5° 赫尔德不等式 设k>1,![]() >1,
>1,![]() ,则
,则
![]() ≤
≤![]()
等号只当f(x)g(x)符号固定且![]() (c为正常数)时成立,当k=k'=2时,就是施瓦兹不等式.
(c为正常数)时成立,当k=k'=2时,就是施瓦兹不等式.
6° 闵可夫斯基不等式 设r>0,则
![]() ≤
≤![]() (r≥1)
(r≥1)
![]() ≥
≥![]()
(r<1, f(x)与g(x)在[a,b]上同号)
等号只当f(x)=cg(x)(c为常数)时成立.
7° 贝塞耳不等式 设![]() (n为正整数)在[a,b]上为一正规正交系:
(n为正整数)在[a,b]上为一正规正交系:
![]()
则
![]() ≤
≤![]()
8° 哈代不等式 设f(x)在[0,∞)上可微且上升,f '(x)连续,f(0)=0,p>1,则
![]()
等号只当f(x)≡0时成立.
三、原函数的求法
1.不定积分法则
![]() ,
,
![]()
![]() (a,b为常数)
(线性运算)
(a,b为常数)
(线性运算)
![]() (变量替换)
(变量替换)
![]() (分部积分)
(分部积分)
![]() (配元积分)
(配元积分)
2.有理分式的积分
[化成基本真分式法] 设R(x)是一个具有实系数的真分式,则R(x)的积分可化成它分解出的基本真分式(第一章,§1)的积分,并且
![]()
式中![]() 仍为一有理函数,并且还是真分式,H(x)一般是超越函数(对数函数和反正切函数).
仍为一有理函数,并且还是真分式,H(x)一般是超越函数(对数函数和反正切函数).
[奥斯特洛格拉特斯基方法] 任一真分式![]() 的积分可以写为
的积分可以写为
![]()
式中![]() ,
,![]() 为真分式,
为真分式,
![]()
![]()
![]()
![]() 和
和![]() 的系数可利用待定系数法从关系式
的系数可利用待定系数法从关系式
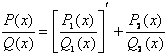
中求出.
3.有理函数积分的变量替换公式表
表中R表示有理函数
|
积分类型 |
变量替换公式 |
|
|
(n为整数)
(m,n为整数) |
式中r为n,m,…的最小公倍数 |
|
|
a>0时
c>0时 |
|
|
|
|
|
|
|
|
(或x=asht,
(或x=acost,
(或x=acht,
|
(或dx=achtdt)
(或dx=-asintdt)
(或dx=-ashtdt)
|
|
积分类型 |
变量替换公式 |
|
|
(式中 |
设m为
|
|
|
|
|
|
|
|
|
|
4.不定积分表
表中略去积分常数,ln g(x)是指ln |g(x)|.
[基本积分表]
|
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
thx |
|
|
cthx |
|
|
sechx |
|
|
cschx |
|
|
|
thx |
|
|
-cthx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或 |
|
|
|
|
|
或 |
|
|
|
|
|
|
[含ax+b的有理式的积分] (![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
(
|
或 或
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分] (
的积分] (![]() )
)
|
|
|
|
|
或 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的有理式的积分]
的有理式的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n>0,p>1) |
|
[含![]() )的有理式的积分]
)的有理式的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n为正整数) |
|
|
(n为正整数) |
|
|
(n为正整数) |
|
|
|
|
|
|
|
|
(n为正整数)
(n为正整数)
|
|
|
|
|
|
|
|
|
|
|
|
|
时,取正号;否则取负号.k为整数 ) |
|
|
时,取正号;否则取负号.k为整数 ) |
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n为正整数) |
|
|
(n为正整数) |
|
|
(n为正整数)
(n为
(n为正整数)
(n为正整数)
|
|
|
|
|
|
|
时,取正号;否则取负号.k为整数 ) |
|
|
时,取负号;否则取正号.k为整数 ) |
|
|
|
|
|
|
|
|
|
[含![]() 和
和![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
式中
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或 |
|
|
或
|
|
f(x) |
|
|
|
|
[含![]() 和
和![]() 的积分]
的积分]
|
f(x) |
|
|
(n为 |
|
|
|
|
|
|
|
|
|
|
|
(n为 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 和
和![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n为正整数) |
|
|
(n为正整数) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或 |
|
|
|
|
|
或 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[含![]() 的积分]
的积分]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(当
当 |
|
|
|
|
|
(当 当 |
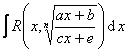

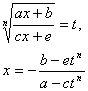
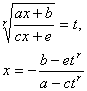
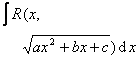
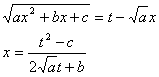
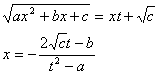
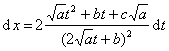
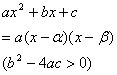
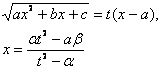
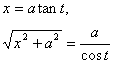
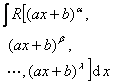
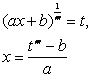
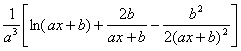


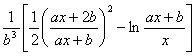
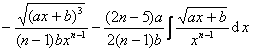
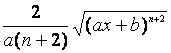
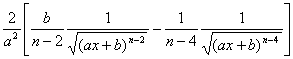
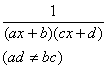
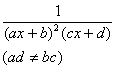
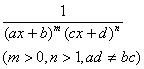
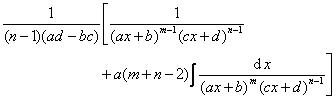
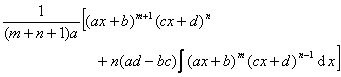

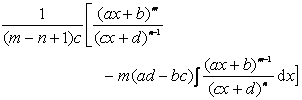
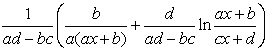
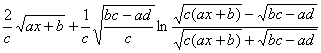
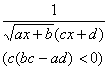
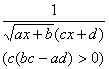
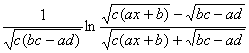
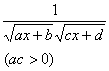
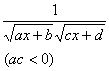
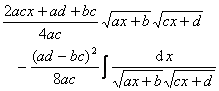
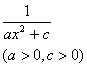
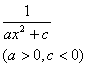
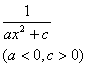
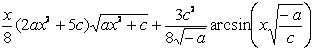
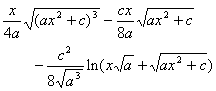

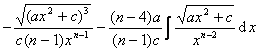
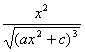 (
(