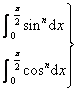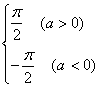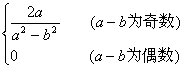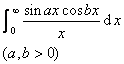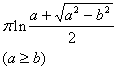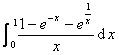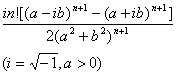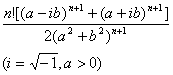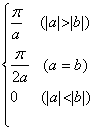四、定积分的求法
[定积分的性质]
![]()
![]()
![]()
![]()
[分部积分法]
![]()
式中![]()
[变量替换法] 设函数![]() 在区间[
在区间[![]() ]上有连续的导数
]上有连续的导数![]() ,同时函数
,同时函数![]() 在区间
在区间![]() 上连续,并且
上连续,并且![]() 从
从![]() 单调地变到
单调地变到![]() ,则
,则
![]()
[利用函数奇偶性求积法]
若![]() 为偶函数,则
为偶函数,则![]()
若![]() 为奇函数,则
为奇函数,则![]()
[利用积分对参数求导法] 设f(x,t)在有界区域![]() 上连续,并且存在连续偏导数
上连续,并且存在连续偏导数![]() ,则当
,则当![]() 时,有
时,有
![]()
例 计算积分![]()
解 设![]()
则 ![]() .因
.因
![]()
![]()
![]()
所以︳![]() .
.
[定积分表]
|
定 积 分 |
定 积 分 值 |
|
|
|
|
|
|
|
|
|
|
定 积 分 |
定 积 分 值 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定 积 分 |
定 积 分 值 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定 积 分 |
定 积 分 值 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定 积 分 |
定 积 分 值 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、广义积分
1. 广义积分的概念
[无穷限广义积分]
设函数f(x)在[a,b]上可积,u>a,![]() <b,u>
<b,u>![]() ,当下列各式右边的极限存在时,
,当下列各式右边的极限存在时,
![]()
![]()
![]()
这时称无穷限广义积分收敛,否则称为发散.
[无界函数的广义积分] 设函数f(x)在给定区间[a,b]上只有一个瑕点x=c,即函数f(x)在x=c点的邻域内无界,而在[a,c-ε]及[c+ε',b]上可积,ε,ε'为任意小的正数,当ε和ε'独立地趋于零,极限
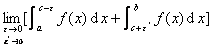 (1)
(1)
存在时,则用上式定义无界函数f(x)从a到b的瑕积分,记作
![]()
[柯西主值] 有时极限(1)不存在,但如果设ε'=ε→0,这个极限(1)存在,就称它为瑕积分![]() 的主值,记作
的主值,记作
![]()
这时称无界函数广义积分在主值意义下收敛,否则称为发散.
[绝对收敛与条件收敛] 如果f(x)的广义积分与|f(x)|的广义积分同时收敛,那末称f(x)的广义积分是绝对收敛, f(x)称为绝对可积;如果仅前者收敛,后者不收敛,那末称f(x)的广义积分是条件收敛.
2. 广义积分收敛判别法
1° ![]() 收敛的充分必要条件是:对任意给定的ε>0,都存在N=N(ε)>0,只要
收敛的充分必要条件是:对任意给定的ε>0,都存在N=N(ε)>0,只要![]() ,就有|
,就有|![]() |<ε.
|<ε.
2° 设f(x)是非负的,则![]() 收敛的充分必要条件是:
收敛的充分必要条件是:
F(u)=![]() 是有界函数.
是有界函数.
3° 设当x→∞时,f(x)=![]() .若p>1,则
.若p>1,则![]() 收敛;若p≤1,则
收敛;若p≤1,则![]() 发散.
发散.
4° 若![]() 收敛,g(x)单调有界(x≥a),则
收敛,g(x)单调有界(x≥a),则![]() 收敛.
收敛.
5° 设f(x)≥0,g(x)≥0,且f(x)≤cg(x)(x≥a,c是一个大于零的常数).若![]() 收敛,则
收敛,则![]() 也收敛;若
也收敛;若![]() 发散,则
发散,则![]() 也发散.
也发散.
6° 无穷级数与广义积分的关系:设f(x)是定义在区间[a,∞)上的一个正的非增连续函数,则级数f(a)+f(a+1)+··+f(a+k)+··与积分![]() 同时收敛或同时发散.
同时收敛或同时发散.
7° 广义积分![]() (以a为瑕点)收敛的充分必要条件是:对任意给定的ε>0,都存在δ(a<δ<b),使当a<u'<u''<δ时|
(以a为瑕点)收敛的充分必要条件是:对任意给定的ε>0,都存在δ(a<δ<b),使当a<u'<u''<δ时|![]() |<ε.
|<ε.
8° 设g(x)有连续的导数,并是恒正的、单调下降的函数,且![]() .若有常数M,使对一切u>a,都有|
.若有常数M,使对一切u>a,都有|![]() |<M,则广义积分
|<M,则广义积分![]() 收敛.
收敛.
六、含参数积分
1. 含参数常义积分
[连续性] 若二元函数f(x,y)在有界区域R(a≤x≤A,b≤y≤B)上有定义且连续,则
![]()
是闭区间[b,B]上的连续函数.
[积分号下的微分法]
若f(x,y)在有界区域R(a≤x≤A,b≤y≤B)上连续,并且存在连续偏导数![]() (x,y),则当b<y<B时,
(x,y),则当b<y<B时,
![]()
一般情况下,当积分限为参数y的可微函数![]() 和
和![]() , 且当b≤y≤B, a≤
, 且当b≤y≤B, a≤![]() ≤A,
≤A,
a≤![]() ≤A时,
≤A时,
![]() (1)
(1)
[积分的求导运算] 以下公式为(1)的特殊情况.
![]()
![]()
![]()
![]()
![]()
[积分号下的积分法]若函数![]() 在有界区域[a≤x≤A,b≤y≤B]上连续,则
在有界区域[a≤x≤A,b≤y≤B]上连续,则
![]()
2 . 含参数广义积分
[一致收敛性] 设函数f(x,y)是定义在区域R(a≤x<∞, y1<y<y2)上的连续函数,若对任意给定的ε>0,都存在只与ε有关的正数B=B(ε),使得当b≥B时,对区间(y1,y2)内一切y不等式
![]()
都成立,则称广义积分![]() 在区间(y1,y2)内一致收敛,并且在该区间内是参数y的连续函数.
在区间(y1,y2)内一致收敛,并且在该区间内是参数y的连续函数.
[一致收敛判别法]
1° 柯西判别积分
![]()
在区间(y1,y2)内一致收敛的充分必要条件是:对任意ε>0,都存在正数B=B(ε),使得当b'>B,b''>B时,对区间(y1,y2)内的一切y,都有
![]()
2° 外尔斯特拉斯判别法 设函数f(x,y)(x的函数)在任一有限区间[a,A]上可积,若存在与参数y无关的函数F(x),它在区间[a,∞)上可积,并且对于区间(y1,y2)内的一切y
|f(x,y)|≤F(x) (x≥a)
则积分
![]()
在区间(y1,y2)内一致收敛.
[对参数的微分法]
若(i)函数f(x,y)在区域R(a≤x<∞, y1<y<y2)内连续,并对参数y可微,(ii)积分![]() 收敛,(iii)积分
收敛,(iii)积分![]() 在区间(y1,y2)内一致收敛,则当y1<y<y2时,
在区间(y1,y2)内一致收敛,则当y1<y<y2时,
![]()
[对参数的积分法]
若函数f (x,y)在区域R(a≤x<∞, y1<y<y2)内连续 ,并且![]() 在区间(y1,y2)内一致收敛,则
在区间(y1,y2)内一致收敛,则
![]()
七、斯蒂尔吉斯积分
[定义] 设在区间[a,b]上给定两个有界函数f(x)和g(x).用任意方法把区间[a,b]分成若干部分,其分点为
a=x0<x1<x2<…< xi<xi+1<…<xn=b
并设λ是Δxi=xi+1-xi(t=0,1,…,n-1)中最大的.在每个小区间![]() 上任取一点
上任取一点![]() ,作和
,作和
σ=![]()
当λ→0时,如果极限![]() 存在,那末这个极限称为函数f(x)对函数g(x)的斯蒂尔吉斯积分,记作
存在,那末这个极限称为函数f(x)对函数g(x)的斯蒂尔吉斯积分,记作
![]()
特别是,当函数g(x)在区间上连续可微时,函数f(x)对g(x)的斯蒂尔吉斯积分就是通常的黎曼积分
![]()
[可积性]
1°若函数f(x)连续,函数g(x)有有界变差,则积分
![]() (1)
(1)
存在.
2°若函数f(x)在区间[a,b]上黎曼可积,函数g(x)满足李普希茨条件:
|g(x')-g(x'')|≤L(x'-x'')
(L为常数,a≤x''<x'≤b)
则积分(1)存在.
3°若函数f(x)在区间[a,b]上黎曼可积,函数g(x)可表示成
g(x)=C+![]()
式中C为常数,函数![]() 在区间[a,b]上绝对可积,则积分(1)存在.
在区间[a,b]上绝对可积,则积分(1)存在.
[积分法则与不等式]
1°积分法则
![]()
![]()
![]()
![]() (k,l为常数)
(k,l为常数)
![]()
(a<c<b,三个积分都存在,当上式右边两个积分存在时,一
般不能推出积分![]() 存在)
存在)
![]() (分部积分公式)
(分部积分公式)
2° 若g(x)在区间[a,b]上为一非减函数,则
![]() ≤
≤![]()
3° 若g(x)在区间[a,b]上为一非减函数,则f(x)≤F(x),则
![]() ≤
≤![]()
八、积分的近似计算
1. 内插求积公式
[等距内插求积一般公式(柯斯特公式)]
![]() ≈(b-a)
≈(b-a)![]()
式中![]() 为等距节点:
为等距节点:
![]() =a+kh k=0,1,2,…,n
=a+kh k=0,1,2,…,n
![]()
![]() 为柯特斯系数(见下表).
为柯特斯系数(见下表).
柯特斯系数表
|
n |
|
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
当区间[a,b]愈小,柯特斯公式所给出的结果愈精确.因此,当区间[a,b]较大时,为了避免采用n值较大的柯特斯公式,常把[a,b]N等分,对其中各个等份应用n值较小的柯特斯公式求积,然后再把各个等份的积分值相加,即得到区间[a,b]上的积分值,如下述的梯形公式(n=1)和辛卜生公式(n=2).
[梯形公式]
![]() ≈
≈![]()
![]() =a+kh, k=1,2,…,N-1
=a+kh, k=1,2,…,N-1
![]()
若![]() ≤M2,则截断误差为
≤M2,则截断误差为
![]() ≤
≤![]()
[辛卜生公式]
![]() ≈
≈![]()
![]() =a+k
=a+k![]() ,
,
![]()
若![]() ≤
≤![]() ,则截断误差为
,则截断误差为
![]() ≤
≤![]()
[龙贝公式] 设
![]()
![]()
=![]()
![]()
则
![]()
![]()
一般地,可适当选取m,使之固定,再增大k,使近似截断误差
![]()
在允许误差范围内即可,这时
![]() ≈
≈![]()
具体计算过程可按下表自左而右,自上而下进行(表中箭头方向表示计算顺序).
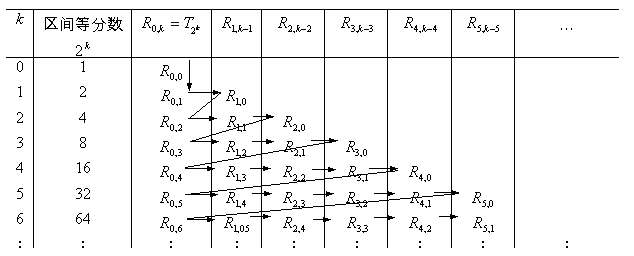 |
例 用龙贝公式计算积分
![]()
![]()
误差不超过0.0000001.
解 这里![]() ,a=0,b=1.可按五步进行计算,结果如下:
,a=0,b=1.可按五步进行计算,结果如下:
(1) ![]()
(2) ![]()
![]()
(3) ![]()
![]()
![]()
(4) ![]()
![]()
![]()
![]()
(5) 可以继续算出
![]() 3.140941614
3.140941614
![]() 3.141592655
3.141592655
![]() 3.141592665
3.141592665
![]() 3.141592643
3.141592643
因为
|![]() -
-![]() |=|3.141592643-3.141592665|<0.0000001
|=|3.141592643-3.141592665|<0.0000001
所以
![]() ≈3.14159264
≈3.14159264
而准确值为
![]()
![]()
在等距内插求积公式中,以辛卜生公式和龙贝公式为好,计算简单 ,便于在电子计算机上实现(都有标准程序),精确度也相当高.特别龙贝公式是采用区间逐次分半的方法,前一次分割得到的函数值在区间分半后仍可利用,具有计算有规律,不需存储柯特斯系数和节点等优点.
但等距内插求积公式不能计算广义积分.广义积分只能用下面的高斯型求积公式来计算.
[不等距内插求积公式(高斯型求积公式 )]
高斯型求积公式为
![]() ≈
≈![]() n=1,2,…
n=1,2,…
式中(a,b)区间可以是有限或无限,w(x)为(a,b)区间内的非负权函数.
-∞≤a≤![]() <
<![]() <…<
<…<![]() <b≤∞
<b≤∞
为求积节点(相应的正交多项式的根),![]() (k=1,2,…,n)为求积系数.f(x)为不超过2n-1次的多项式时,上述求积公式(1)成为等式.
(k=1,2,…,n)为求积系数.f(x)为不超过2n-1次的多项式时,上述求积公式(1)成为等式.
下面列出几种特例.
1°![]()
(-1<θ<1)
式中![]() 为勒让德多项式
为勒让德多项式![]() (见第十二章,§2,一)的根.
(见第十二章,§2,一)的根.
2°![]()
(-1<θ<1)
式中![]() 为第一类契贝谢夫多项式
为第一类契贝谢夫多项式![]() (见第十二章,§2,二)的根.
(见第十二章,§2,二)的根.
它也可表为
![]()
3° ![]()
(-1<θ<1)
式中![]() 为第二类契贝谢夫多项式
为第二类契贝谢夫多项式![]() (见第十二章,§2,三)的根.
(见第十二章,§2,三)的根.
4°![]()
(-1<θ<1)
5°![]()
2. 高斯型求积公式的求积节点和求积系数表
[高斯求积公式]
![]()
式中![]() 为勒让德多项式
为勒让德多项式![]() 的根.
的根.
|
n |
求积节点 |
求积系数 |
|
2 |
|
1 |
|
3 |
0
|
0.88888 88889 0.55555 55556 |
|
4 |
|
0.65214 51549 0.34785 48451 |
|
5 |
0
|
0.56888 88889 0.47862 86705 0.23692 68851 |
|
6 |
|
0.46791 39346 0.36076 15731 0.17132 44924 |
|
7 |
0
|
0.41795 91837 0.38183 00505 0.27970 53915 0.12948 49662 |
|
8 |
|
0.36268 37834 0.31370 66459 0.22238 10345 0.10122 85363 |
|
n |
求积节点 |
求积系数 |
|
9 |
0
|
0.33023 93550 0.31234 70770 0.26061 06964 0.18064 81607 0.08127 43884 |
|
10 |
|
0.29552 42247 0.26926 67193 0.21908 63625 0.14945 13492 0.06667 13443 |
[勒贝陶求积公式]
![]()
式中![]() 为
为![]() 的根.
的根.
|
n |
求积节点 |
求积系数 |
|
3 |
0
|
0.33333 333 1.33333 333 |
|
4 |
|
0.16666 667 0.83333 333 |
|
5 |
0 |
0.10000 000 0.54444 444 0.71111 111 |
|
6 |
|
0.06666 667 0.37847 496 0.55485 838 |
|
7 |
0
|
0.04761 904 0.27682 604 0.43174 538 0.48761 904 |
|
8 |
|
0.03571 428 0.21070 422 0.34112 270 0.41245 880 |
|
9 |
0
|
0.02777 77778 0.16549 53616 0.27453 87126 0.34642 85110 0.37151 92744 |
|
10 |
|
0.02222 22222 0.13330 59908 0.22488 93420 0.29204 26836 0.32753 97612 |
[拉盖尔求积公式]
![]()
![]()
式中![]() 为拉盖尔多项式
为拉盖尔多项式![]() (见第十二章,§2,四)的根.
(见第十二章,§2,四)的根.
|
n |
求积节点 |
求积系数 |
|
|
2 |
0.58578 64376 3.41421 35624 |
(-1)8.53553 39059* (-1)1.46446 60941 |
1.53332 60331 4.45095 73351 |
|
3 |
0.41577 45568 2.29428 03603 6.28994 50829 |
(-1)7.11093 00993 (-1)2.78517 73357 (-1)1.03892 56502 |
1.07769 28593 2.76214 29619 5.60109 46254 |
|
4 |
0.32254 76896 1.74576 11012 4.53662 02969 9.39507 09123 |
(-1)6.03154 10434 (-1)3.57418 69244 (-2)3.88879 08515 (-4)5.39294 70556 |
0.83273 91238 2.04810 24385 3.63114 63058 6.48714 50844 |
|
5 |
0.26356 03197 1.41340 30591 3.59642 57710 7.08581 00059 12.64080 08443 |
(-1)5.21755 61058 (-1)3.98666 81108 (-2)7.59424 49582 (-3)3.61175 86799 (-5)2.33699 72386 |
0.67909 40422 1.63848 78736 2.76944 32424 4.31565 69009 7.21918 63544 |
|
6 |
0.22284 66042 1.18893 21017 2.99273 63261 5.77514 35691 9.8374674184 15.98287 39806 |
(-1) 4.58964 67395 (-1)4.17000 83077 (-1)1.13373 38207 (-2)1.03991 97453 (-4)2.61017 20282 (-7)8.98547 90643 |
0.57353 55074 1.36925 25907 2.26068 45934 3.35052 45824 4.88682 68002 7.84901 59456 |
|
7 |
0.19304 36766 1.02666 48953 2.56787 67450 4.90035 30845 8.18215 34446 12.73418 02918 19.39572 78623 |
(-1)4.09318 95170 (-1)4.21831 27786 (-1)1.47126 34866 (-2)2.06335 14469 (-3)1.07401 01433 (-5)1.58654 64349 (-8)3.17031 54790 |
0.49647 75975 1.17764 30609 1.91824 97817 2.77184 86362 3.84124 91225 5.38067 82079 8.40543 24868 |
|
8 |
0.17027 96323 0.90370 17768 2.25108 66299 4.26670 01703 7.04560 54024 10.75851 60102 15.74067 86413 22.86313 17369 |
(-1)3.69188 58934 (-1)4.18786 78081 (-1)1.75794 98664 (-2)3.33434 92261 (-3)2.79453 62352 (-5)9.07650 87734 (-7)8.48574 67163 (-9)1.04800 11749 |
0.43772 34105 1.03386 93477 1.66970 97657 2.37692 47018 3.20854 09134 4.26857 55108 5.81808 33687 8.90622 62153 |
|
9 |
0.15232 22277 0.80722 00227 2.00513 51556 3.78347 39733 6.20495 67779 9.37298 52517 13.46623 69111 18.83359 77890 26.37407 18909 |
(-1)3.36126 42180 (-1)4.11213 98042 (-1)1.99287 52537 (-2)4.74605 62766 (-3)5.59962 66108 (-4)3.05249 76709 (-6)6.59212 30261 (-8)4.11076 93304 (-11)3.29087 40304 |
0.39143 11243 0.92180 50285 1.48012 79099 2.08677 08076 2.77292 13897 3.59162 60681 4.64876 60021 6.21227 54198 9.36321 82377 |
*![]() 表示数
表示数![]() ,其他类同,
,其他类同,![]() .
.
[埃尔米特求积公式]
![]()
![]()
式中![]() 为埃尔米特多项式
为埃尔米特多项式![]() (见第十二章,§2,五)的根.
(见第十二章,§2,五)的根.
|
n |
求积节点 |
求积系数 |
|
|
2 |
|
(-1)8.86226 92545*
|
1.46114 11827
|
|
3 |
0
|
(0)1.18163 59006 (-1)2.95408 97515
|
1.18163 59006 1.32393 11752
|
|
4 |
|
(-1)8.04914 09001 (-2)8.13128 35447
|
1.05996 44829 1.24022 58177
|
|
5 |
0
|
(-1)9.45308 72048 (-1)3.93619 32315 (-2)1.99532 42059
|
0.94530 87205 0.98658 09968 1.18148 86255
|
|
6 |
|
(-1)7.24629 59522 (-1)1.57067 32032 (-3)4.53000 99055
|
0.87640 13344 0.93558 05576 1.13690 83327
|
|
7 |
0
|
(-1)8.10264 61756 (-1)4.25607 25261 (-2)5.45155 82819 (-4)9.7178124510
|
0.81026 46176 0.82868 73033 0.89718 46002 1.10133 07296
|
|
8 |
|
(-1)6.61147 01256 (-1)2.07802 32582 (-2)1.70779 83007 (-4)1.99604 07221
|
0.76454 41287 0.79289 00484 0.86675 26066 1.07193 01443
|
|
9 |
0
|
(-1)7.20235 21561 (-1)4.32651 55900 (-2)8.84745 27394 (-3)4.94362 42755 (-5)3.96069 77263
|
0.72023 52156 0.73030 24528 0.76460 81251 0.84175 27015 1.04700 35810
|
|
10 |
|
(-1)6.10862 63374 (-1)2.40138 61108 (-2)3.38743 94456 (-3)1.34364 57468 (-6)7.64043 28552
|
0.68708 18540 0.70329 63231 0.74144 19319 0.82066 61264 1.02545 16914
|
* ![]() 表示数
表示数![]() 其他类同.
其他类同.