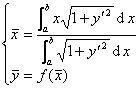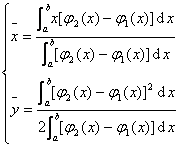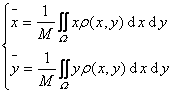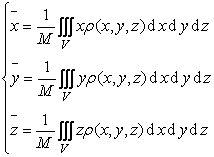§3 积分的应用
一、求面积
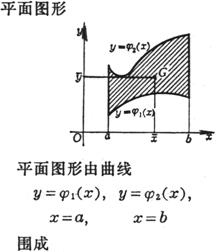
[平面图形面积计算公式]
|
图 形 |
面 积 S |
|
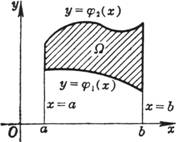
曲边梯形 |
|
|
|
|
|
图 形 |
面 积 S |
|
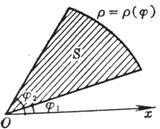
扇形
|
|
|
|
|
|
|
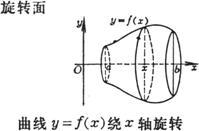
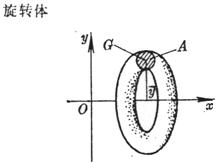
S= 或 S=2 式中 G到旋转轴的距离. |
|
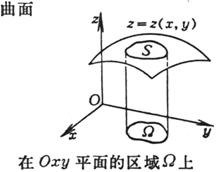
曲面 在 |
式中
|
|
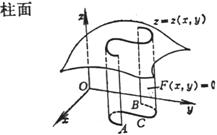
柱面
|
式中C为柱面的准线,ds为曲线C(A,B)上的弧的微 分 .
|
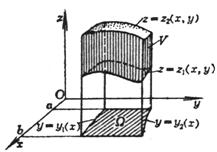
二、求体积
|
图 形 |
体 积V |
|
|
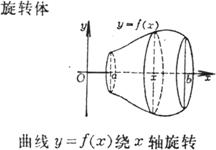
式中 |
|
|
式中A为所旋转的平面图形的面积, |
|
|
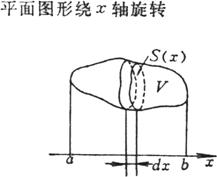
式中S(x)为垂直于x轴的截面面积 |
|
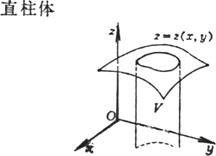
在曲面 |
|
|
空间区域V由下列曲面围成:
|
式中 |
三、n维空间中凸体体积公式
n维空间的点的坐标为(![]() ).所谓n维空间中的凸体
).所谓n维空间中的凸体![]() ,是指
,是指![]() 中任意两点A和B的连线仍在
中任意两点A和B的连线仍在![]() 中,即设A=
中,即设A=![]() B=
B=![]() ,若A,B∈
,若A,B∈![]() ,则点
,则点![]() .其中
.其中
![]() , i=1,2,…,n
, i=1,2,…,n
下面列出几种凸体体积的计算公式.
[单纯形] 已知n维空间中的n+1个点![]() ,包含这n+1个点的最小凸体称为由
,包含这n+1个点的最小凸体称为由![]() 张成的单纯形,记作
张成的单纯形,记作![]() ,若设
,若设![]() 的n个坐标为
的n个坐标为
(![]() )
i=1,2,…,n+1
)
i=1,2,…,n+1
则单纯形![]() 的体积
的体积

n=2时为三角形,n=3时为四面体.
[超立方体]
![]() : |
: |![]() |≤
|≤![]() ,
i=1,2,…,n
,
i=1,2,…,n
V=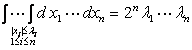
[广义八面体]
1°![]() 1:
1:![]() ≤r,
≤r, ![]() >0,
i=1,2,…,n
>0,
i=1,2,…,n
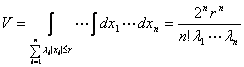
2°![]() 2:
2:![]() ≤r,
≤r, ![]() >0,
>0,
![]() >0,i=1,2,…,n-1
>0,i=1,2,…,n-1
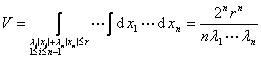
[n维球体]
![]() :
:![]()
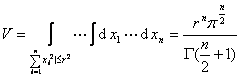
[凸体的线形变换] 设有线性变换
![]() =
=![]() , i=1,2,…,n
, i=1,2,…,n
J=det(dij)≠0
将凸体R映成![]() ,则
,则![]() 的体积为
的体积为
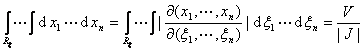
这里![]()
![]() 为该线性变换的雅可比式.
为该线性变换的雅可比式.
四、求重心
[平面图形几何重心坐标的计算公式]
|
图 形 |
几何重心 |
|
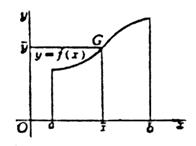
平面曲线
|
|
|
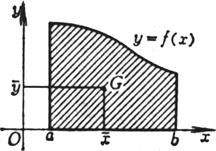
曲边梯形
|
|
|
|
|
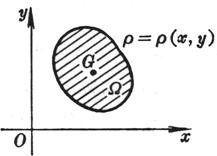
[物体总质量与重心坐标的计算公式]
|
物体形状及密度 |
总质量M与重心 |
|
薄板
|
|
|
物体形状及密度 |
总质量M与重心 |
|
|
|
|
|
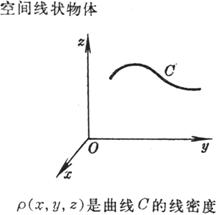
式中ds 为弧的微分,以上积分为曲线积分。 |
五、求转动惯量
[薄板的转动惯量] 设Oxy平面内薄板Ω的密度为ρ=ρ(x,y),对于x轴,y轴,原点O的转动惯量分别为![]() ,则
,则
![]()
![]()
![]()
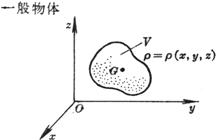
[一般物体的转动惯量] 设物体V的密度ρ=ρ(x,y,z).若物体对于坐标平面的转动惯量分别为![]() ;物体对于某轴l的转动惯量为
;物体对于某轴l的转动惯量为![]() ;物体对于坐标轴的转动惯量分别
;物体对于坐标轴的转动惯量分别![]() ;物体对于原点的转动惯量为
;物体对于原点的转动惯量为![]() ,则
,则
![]()
![]()
![]()
![]()
式中r为物体的动点到轴l的距离.
![]()
![]()
![]()
|
|
六、求流体压力
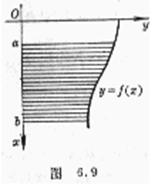
设流体接触面的边缘曲线为y=f(x)(图6.9),流体密度为w,则单侧压力
![]()
七、求变力所做的功
1°若s为路程,f(s)为变力,则
![]()
2°若s为路程,运动路线为C,f(x,y)为变力,θ为变力f与路线C切线的夹角,则
![]()
3°若变力沿坐标轴的三个分力分别为P(x,y,z),Q(x,y,z),R(x,y,z),C为空间运动路线,则
![]()